3.4.3. The Fundamental Ideal
The astute observer will note that the contact manifold ${C_m}$ containing the variables of the PDE system will not actually represent the PDE system until ${F^a}$ is employed to connect them together properly, forming a sub-manifold. We have abstracted the relevant variables into EDS space ${T^*}\left( {{C_m}} \right)$ via the set of contact 1-forms. It remains to embody the PDE system in an EDS construct as well. Including it in some form of an ideal along with the contact 1-forms and possibly their differentials (to “close” the ideal) will set us up to apply the isovector formalism introduced earlier to “solve” for the symmetries of the PDE system represented by those isovectors. Suhubi takes us through a long tortuous path to two candidates for such a “fundamental” ideal. These are so-called ${m^{th}}$-order (closed) ideal candidates:
\begin{equation}{\mathcal{F}_m} = \bar {\mathcal{F}}\left( {{\sigma ^\alpha },\sigma _{{i_1}}^\alpha ,\sigma _{{i_1}{i_2}}^\alpha , \ldots ,\sigma _{{i_1}{i_2} \ldots {i_{m - 1}}}^\alpha ;d\sigma _{{i_1}{i_2} \ldots {i_{m - 1}}}^\alpha ;d{F^a}} \right)\notag\end{equation}
and
\begin{equation}{\mathcal{F}_m} = \bar {\mathcal{F}}\left( {{\sigma ^\alpha },\sigma _{{i_1}}^\alpha ,\sigma _{{i_1}{i_2}}^\alpha , \ldots ,\sigma _{{i_1}{i_2} \ldots {i_{m - 1}}}^\alpha ;d\sigma _{{i_1}{i_2} \ldots {i_{m - 1}}}^\alpha ;{\omega ^a}} \right)\notag\end{equation}
where
\begin{equation}{\omega ^a} \equiv {F^a}\mu \equiv {F^a}d{x^1} \wedge d{x^2} \wedge \ldots \wedge d{x^n}\notag\end{equation}
Comments: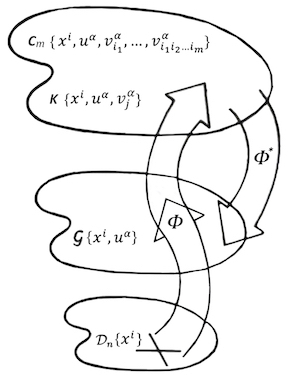
We are going to jump to a restatement (with symbol substitutions) of Suhubi Theorem 5.12.5 as it applies to development in his section 9.4:
Theorem 5.12.5 (restated) A vector V is an isovector of the ideal ${\mathcal{I}}\left( {{\sigma ^\alpha },{\omega ^a}} \right),\;$ where ${\text{deg}}\left( {{\sigma ^\alpha }} \right) < k$ and ${\text{deg}}\left( {{\omega ^a}} \right) \geqslant k$, iff
(i) it is an isovector of $\bar {\mathcal{I}}\left( {{\sigma ^\alpha }} \right)$, and
(ii) ${\mathcal{L}_V}{\omega ^a} \in \;\bar {\mathcal{I}}\left( {{\sigma ^\alpha },{\omega ^a}} \right)$.
We will apply this theorem to the second of our fundamental ideals. A great deal of progress can be made by breaking the process into two steps suggested by the above theorem.
Part (i). First, we take ${\text{deg}}\left( {{\sigma ^\alpha }} \right) = 1$ and note that finding the isovectors of such an ideal is equivalent to finding the isovectors of its closure by Suhubi’s Theorem 5.12.4: If an ideal ${\mathcal{I}}$ is generated by forms of the same degree, then isovectors of the ideals ${\mathcal{I}}$ and $\bar {\mathcal{I}}$ are coincident.
We apply the first part of the theorem to the contact ideal ${\mathcal{I}_m}\left( {{\sigma ^\alpha },\sigma _{{i_1}}^\alpha ,\sigma _{{i_1}{i_2}}^\alpha , \ldots ,\sigma _{{i_1}{i_2} \ldots {i_{m - 1}}}^\alpha } \right)$ and define a “generic” isovector as follows:
\begin{equation}V = {X^i}\frac{\partial }{{\partial {x^i}}} + \mathop \sum \limits_{r = 0}^m V_{{i_1}{i_2} \ldots {i_r}}^\alpha \frac{\partial }{{\partial v_{{i_1}{i_2} \ldots {i_r}}^\alpha }}\label{Vir}\end{equation}
This symbolism is used throughout the Suhubi process. Note the use of the summation symbol rather than relying on the Einstein summation convention due to the differing index runs. We then require the Lie derivative of all generators of the ideal with respect to this vector be expressible as a linear combination of the generators:
\begin{equation}{\mathcal{L}_V}\sigma _{{i_1}{i_2} \ldots {i_k}}^\alpha = \mathop \sum \limits_{r = 0}^m \lambda _{\beta \;{i_1} \ldots {i_k}}^{\alpha \;{j_1} \ldots {j_r}}\sigma _{{j_1} \ldots {j_r}}^\beta ,\;k = 0, \ldots ,m - 1\notag\end{equation}
where the $\lambda _{\beta \;{i_1} \ldots {i_k}}^{\alpha \;{j_1} \ldots {j_r}}$coefficients are functions since the result of the LHS is 1-forms. He proceeds over the course of 10 pages to insert the generic form for V into this operation, match sides of the equality, determine solution modes based on values of N (number of dependent variables) and finally expresses the result as Theorem 9.3.1, the first part of which is shown next.
Theorem 9.3.1(first part). The isovector coefficients $V_{{i_1}{i_2} \ldots {i_r}}^\alpha $ in \eqref{Vir} satisfy the recursion relation
\begin{equation}V_{{i_1}{i_2} \ldots {i_k},i}^\alpha = D_i^{\left( k \right)}\left( {V_{{i_1}{i_2} \ldots {i_k}}^\alpha - v_{{i_1}{i_2} \ldots {i_k},j}^\alpha {X^j}} \right),\;0 \leqslant k \leqslant m - 1\label{Viki}\end{equation}
\begin{equation}D_i^{\left( k \right)} = \frac{\partial }{{\partial {x^i}}} + v_i^\alpha \frac{\partial }{{\partial {u^\alpha }}} + \mathop \sum \limits_{r = 1}^k v_{{i_1}{i_2} \ldots {i_r},i}^\alpha \frac{\partial }{{\partial v_{{i_1}{i_2} \ldots {i_r}}^\alpha }}\notag\end{equation}
This differential operator also has a recursion relation
\begin{equation}D_i^{\left( 0 \right)} = \frac{\partial }{{\partial {x^i}}} + v_i^\alpha \frac{\partial }{{\partial {u^\alpha }}},\;\;D_i^{\left( {k + 1} \right)} = D_i^{\left( k \right)} + v_{{i_1}{i_2} \ldots {i_{k + 1}},i}^\alpha \frac{\partial }{{\partial v_{{i_1}{i_2} \ldots {i_{k + 1}}}^\alpha }}\notag\end{equation}
Incidentally, these can be written more compactly using the multi-index $J\left( k \right) \equiv {i_1}{i_2} \ldots {i_k}$ from Chapter 2:
\begin{equation}V_{J\left( k \right),i}^\alpha = D_i^{\left( k \right)}\left( {V_{J\left( k \right)}^\alpha - v_{J\left( k \right),j}^\alpha {X^j}} \right),\;0 \leqslant k \leqslant m - 1\notag\end{equation}
\begin{equation}D_i^{\left( k \right)} = \frac{\partial }{{\partial {x^i}}} + v_i^\alpha \frac{\partial }{{\partial {u^\alpha }}} + \mathop \sum \limits_{r = 1}^k v_{J\left( r \right),i}^\alpha \frac{\partial }{{\partial v_{J\left( r \right)}^\alpha }}\notag\end{equation}
\begin{equation}D_i^{\left( 0 \right)} = \frac{\partial }{{\partial {x^i}}} + v_i^\alpha \frac{\partial }{{\partial {u^\alpha }}},\;\;D_i^{\left( {k + 1} \right)} = D_i^{\left( k \right)} + v_{J\left( {k + 1} \right),j}^\alpha \frac{\partial }{{\partial v_{J\left( {k + 1} \right)}^\alpha }}\notag\end{equation}
Let us compute $V$ for $m = 2$.
\begin{equation}V = {X^i}\frac{\partial }{{\partial {x^i}}} + V_0^\alpha \frac{\partial }{{\partial v_0^\alpha }} + V_{{i_1}}^\alpha \frac{\partial }{{\partial v_{{i_1}}^\alpha }} + V_{{i_1}{i_2}}^\alpha \frac{\partial }{{\partial v_{{i_1}{i_2}}^\alpha }} = {X^i}\frac{\partial }{{\partial {x^i}}} + {U^\alpha }\frac{\partial }{{\partial {u^\alpha }}} + V_{{i_1}}^\alpha \frac{\partial }{{\partial v_{{i_1}}^\alpha }} + V_{{i_1}{i_2}}^\alpha \frac{\partial }{{\partial v_{{i_1}{i_2}}^\alpha }}\label{V0}\end{equation}
where the $r = 0$ term has the indicated interpretation. Now the next term is
\begin{equation}V_i^\alpha \equiv V_{0,i}^\alpha = D_i^{\left( 0 \right)}\left( {V_0^\alpha - v_{0,j}^\alpha {X^j}} \right) = \left( {\frac{\partial }{{\partial {x^i}}} + v_i^\beta \frac{\partial }{{\partial {u^\beta }}}} \right)\left( {{U^\alpha } - v_j^\alpha {X^j}} \right) = \frac{{\partial {U^\alpha }}}{{\partial {x^i}}} - v_j^\alpha \frac{{\partial {X^j}}}{{\partial {x^i}}} + v_i^\beta \frac{{\partial {U^\alpha }}}{{\partial {u^\beta }}} - v_i^\beta v_j^\alpha \frac{{\partial {X^j}}}{{\partial {u^\beta }}}\label{Vi}\end{equation}
in agreement with Suhubi (9.3.21). Note how we move the operation $\partial /\partial {x^i}$ past the “independent variable” $v_j^\alpha $ as we are in the contact manifold. Note also the replacement of dummy variable $\alpha $ with $\beta $ to avoid confusion. The next (last) term starts to get complicated:
\begin{equation}V_{{i_1}{i_2}}^\alpha = D_{{i_2}}^{\left( 1 \right)}\left( {V_{{i_1}}^\alpha - v_{{i_1},j}^\alpha {X^j}} \right)\notag\end{equation}
\begin{equation}D_{{i_2}}^{\left( 1 \right)} = D_{{i_2}}^{\left( 0 \right)} + v_{{i_1},{i_2}}^\alpha \frac{\partial }{{\partial v_{{i_1}}^\alpha }} = \frac{\partial }{{\partial {x^{{i_2}}}}} + v_{{i_2}}^\beta \frac{\partial }{{\partial {u^\beta }}} + v_{{i_1},{i_2}}^\beta \frac{\partial }{{\partial v_{{i_1}}^\beta }}\notag\end{equation}
having replaced dummy variable $i$ with ${i_2}$. Then
\begin{equation}V_{{i_1}{i_2}}^\alpha = \left( {\frac{\partial }{{\partial {x^{{i_2}}}}} + v_{{i_2}}^\beta \frac{\partial }{{\partial {u^\beta }}} + v_{{i_1}{i_2}}^\beta \frac{\partial }{{\partial v_{{i_1}}^\beta }}} \right)\left( {\frac{{\partial {U^\alpha }}}{{\partial {x^i}}} - v_j^\alpha \frac{{\partial {X^j}}}{{\partial {x^i}}} + v_i^\beta \frac{{\partial {U^\alpha }}}{{\partial {u^\beta }}} - v_i^\beta v_j^\alpha \frac{{\partial {X^j}}}{{\partial {u^\beta }}} - v_{{i_1}j}^\alpha {X^j}} \right)\label{Vii}\end{equation}
Note that we have replaced $v_{{i_1},{i_2}}^\alpha $, for example, with $v_{{i_1}{i_2}}^\alpha $ to make explicit their roles as “independent variables” in contact space per Suhubi (9.26). We will not expand this term, but pause to reflect on the remaining vector coefficients for such an $m = 2$ case. Equations \eqref{V0}, \eqref{Vi} and \eqref{Vii} give the form of the isovector of the contact ideal in terms of functions ${X^j}$ and ${U^\alpha }$. The second part of Suhubi’s Theorem 9.3.1 addresses these functions for the case of a single or multiple dependent variables in the original PDE system.
Theorem 9.3.1(second part) For $N > 1$, the coefficients ${X^i}$ and ${U^\alpha }$ are arbitrary functions of $\left( {{x^i},{u^\alpha }} \right)$. For $N = 1$ (dropping the $\alpha $ superscript here) these functions are connected by a single “universal” function $F\left( {{x^i},u,{v_j}} \right)$, from which both ${X^i}$ and $U$ can be computed thusly:
\begin{equation}{X^i} = - \frac{{\partial F}}{{\partial {v_i}}}\;{\text{and}}\;U = F - {v_i}\frac{{\partial F}}{{\partial {v_i}}},\;m = 1\notag\end{equation}
In Suhubi equations (9.3.25) and (9.3.26) he provides extensions of the above for higher ($m > 1$) components of the isovectors, with the first (for $m = 2$) as follows:
\begin{equation}{V_i} = \frac{{\partial F}}{{\partial {x^i}}} + {v_i}\frac{{\partial F}}{{\partial u}}\notag\end{equation}
So far the results are quite sterile in that we have found the isovector of the contact ideal without any information about the PDE system itself per condition (i) of Theorem 5.12.5 (restated), and repeated here:
Theorem 5.12.5 (restated) A vector V is an isovector of the ideal ${\mathcal{I}}\left( {{\sigma ^\alpha },{\omega ^a}} \right),\;$where ${\text{deg}}\left( {{\sigma ^\alpha }} \right) < k$ and ${\text{deg}}\left( {{\omega ^a}} \right) \geqslant k$, iff
(i) it is an isovector of $\bar {\mathcal{I}}\left( {{\sigma ^\alpha }} \right)$, and
(ii) ${\mathcal{L}_V}{\omega ^a} \in \;\bar {\mathcal{I}}\left( {{\sigma ^\alpha },{\omega ^a}} \right)$
We now turn to the second part of the theorem. The full ideal for which we seek isovectors is the fundamental ideal introduced earlier:
\begin{equation}{\mathcal{F}_m} = \bar {\mathcal{F}}\left( {{\sigma ^\alpha },\sigma _{{i_1}}^\alpha ,\sigma _{{i_1}{i_2}}^\alpha , \ldots ,\sigma _{{i_1}{i_2} \ldots {i_{m - 1}}}^\alpha ;d\sigma _{{i_1}{i_2} \ldots {i_{m - 1}}}^\alpha ;{\omega ^a}} \right)\notag\end{equation}
where\begin{equation}{\omega ^a} \equiv {F^a}\mu \equiv {F^a}d{x^1} \wedge d{x^2} \wedge \ldots \wedge d{x^n},\;a = 1, \ldots ,A\notag\end{equation}
You many notice that part (i) of Theorem 5.12.5 (restated) has ignored the closure of the contact ideal belabored above. Suhubi explains (by his Theorem 5.12.4) that since that ideal is generated by forms of the same degree its isovectors will be the same as those of its closure $\bar {\mathcal{I}}$ so the results above will still apply as we move to the next step. Proceeding, let us now compute
\begin{equation}{\mathcal{L}_V}\left( {{\omega ^a}} \right) = \left\langle {V,d{\omega ^a}} \right\rangle + d\left\langle {V,{\omega ^a}} \right\rangle \;\notag\end{equation}
Expanding the LHS this becomes
\begin{equation}{\mathcal{L}_V}\left( {{\omega ^a}} \right) = V\left( {{F^a}} \right)\mu + {F^a}d{X^i} \wedge {\mu _i}\label{Vexp}\end{equation}
where\begin{equation}{\mu _i}\left\langle {\frac{\partial }{{\partial {x^i}}},\mu } \right\rangle = {\left( { - 1} \right)^{i + 1}}d{x^1} \wedge \ldots \wedge d{x^{i - 1}} \wedge d{x^{i + 1}} \wedge \ldots \wedge d{x^n}\notag\end{equation}
First term: we start with \begin{equation}d{\omega ^a} = d\left( {{F^a}\mu } \right) = d{F^a} \wedge d{x^1} \wedge d{x^2} \wedge \ldots \wedge d{x^n}\notag\end{equation}since $d\mu = 0$. Then \begin{equation}\left\langle {V,d{\omega ^a}} \right\rangle = \left\langle {V,d{F^a} \wedge \mu } \right\rangle = \left\langle {V,d{F^a}} \right\rangle \wedge \mu - d{F^a} \wedge \left\langle {V,\mu } \right\rangle = V\left( {{F^a}} \right)\mu - {X^i}d{F^a} \wedge {\mu _i}\notag\end{equation} Note the last term introduces the symbol ${\mu _i}$ which comes from \begin{equation}\left\langle {\frac{\partial }{{\partial {x^i}}},d{x^1} \wedge d{x^2} \wedge \ldots \wedge d{x^n}} \right\rangle = {\left( { - 1} \right)^{i + 1}}d{x^1} \wedge d{x^2} \wedge d{x^{i - 1}} \wedge d{x^{i + 1}} \wedge \ldots \wedge d{x^n} \equiv {\mu _i}\notag\end{equation} Replacement of $\left\langle {V,d{F^a}} \right\rangle $ with $V\left( {{F^a}} \right)$ (vector operating on a function) is demonstrated as follows: \begin{equation}\left\langle {V,d{F^a}} \right\rangle = \left\langle {{X^i}\frac{\partial }{{\partial {x^i}}} + {U^\alpha }\frac{\partial }{{\partial {u^\alpha }}} + \mathop \sum \limits_{r = 1}^m V_{{i_1}{i_2} \ldots {i_r}}^\alpha \frac{{\partial {F^a}}}{{\partial v_{{i_1}{i_2} \ldots {i_r}}^\alpha }},\frac{{\partial {F^a}}}{{\partial {x^i}}}d{x^i} + \frac{{\partial {F^a}}}{{\partial {u^\alpha }}}d{u^\alpha } + \mathop \sum \limits_{r = 1}^m \frac{{\partial {F^a}}}{{\partial v_{{i_1}{i_2} \ldots {i_r}}^\alpha }}dv_{{i_1}{i_2} \ldots {i_r}}^\alpha } \right\rangle \notag\end{equation} \begin{equation}\left\langle {V,d{F^a}} \right\rangle = \left\langle {{X^i}\frac{{\partial {F^a}}}{{\partial {x^i}}} + {U^\alpha }\frac{{\partial {F^a}}}{{\partial {u^\alpha }}} + \mathop \sum \limits_{r = 1}^k V_{{i_1}{i_2} \ldots {i_r}}^\alpha \frac{{\partial {F^a}}}{{\partial v_{{i_1}{i_2} \ldots {i_r}}^\alpha }}} \right\rangle = V\left( {{F^a}} \right)\notag\end{equation} The second term \begin{equation}d\left\langle {V,{\omega ^a}} \right\rangle = d\left\langle {V,{F^a}\mu } \right\rangle = d\left( {{F^a}\left\langle {V,\mu } \right\rangle \;} \right) = d\left( {{F^a}{X^i}{\mu _i}\;} \right) = {F^a}d{X^i} \wedge {\mu _i} + {X^i}d{F^a} \wedge {\mu _i}\;\notag\end{equation} Combining these results: \begin{equation}{\mathcal{L}_V}\left( {{\omega ^a}} \right) = V\left( {{F^a}} \right)\mu - {X^i}d{F^a} \wedge {\mu _i} + {F^a}d{X^i} \wedge {\mu _i} + {X^i}d{F^a} \wedge {\mu _i} = V\left( {{F^a}} \right)\mu + {F^a}d{X^i} \wedge {\mu _i}\;\color{blue}\blacksquare \notag\end{equation}
To satisfy the second part Theorem 5.12.5 (restated) we require ${\mathcal{L}_V}{\omega ^a} \in \;{\bar {\mathcal{I}}_m}$:
\begin{equation}V\left( {{F^a}} \right)\mu + {F^a}d{X^i} \wedge {\mu _i} = \mathop \sum \limits_{r = 0}^{m - 1} \lambda _\beta ^{a\;{i_1} \ldots {i_r}} \wedge \sigma _{{i_1} \ldots {i_r}}^\beta + \Lambda _\beta ^{a\;{i_1} \ldots {i_{m - 1}}} \wedge d\sigma _{{i_1} \ldots {i_{m - 1}}}^\beta + \lambda _\beta ^a{\omega ^\beta }\notag\end{equation}
The coefficient forms on the RHS are of appropriate degree to match the LHS. Note Suhubi uses both “a” and “$\alpha $” on the same symbols so be careful. Recall the indices above run as follows: $a = 1, \ldots ,A,\;\;\;i = 1, \ldots ,n\;\;{\text{and}}\;\alpha = 1, \ldots ,N$. [At some point Suhubi’s development assumes $A = N$; that is, the problem is sufficiently defined with the same number of PDEs as dependent variables, so his choice of similar looking indices may not have been accidental.]
The program has us then substituting the explicit function ${F^a}$ in the LHS, expanding everything to the index running limits and equating coefficients of matching forms on either side. This results in a set of determining equations (DEs) for the components of V (after eliminating the coefficients on the RHS), expressible in terms of ${X^i}$ and ${U^\alpha }$ for the $N > 1$ case, and the universal function $F\left( {{x^i},u,{v_j}} \right)$ for $N = 1$.
In the case of the 1D heat equation the relationships are:
\begin{equation}U = F - {v_1}\frac{{\partial F}}{{\partial {v_1}}} - {v_2}\frac{{\partial F}}{{\partial {v_2}}}\notag\end{equation}
\begin{equation}{X^1} = - \frac{{\partial F}}{{\partial {v_1}}},\;\;{X^2} = - \frac{{\partial F}}{{\partial {v_2}}}\notag\end{equation}
\begin{equation}{V_1} = \frac{{\partial F}}{{\partial x}} + {v_1}\frac{{\partial F}}{{\partial u}},\;\;\;\;\;\;\;{V_2} = \frac{{\partial F}}{{\partial t}} + {v_2}\frac{{\partial F}}{{\partial u}}\notag\end{equation}
where the universal function is found by solving the determining equations (DEs). In the APPENDIX 3.4B (HeatNonBalance) we apply this process to the heat equation, whose symmetry vectors (isovectors) we have found before.